| Definitions | 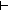 es.P(es), es.P(es),  x:A. B(x), x:A. B(x),   b, sendMinimalR{$a:ut2, $tg:ut2}(T; t; l; ds1; ds2; P; Q; d1; d2; f), lnk-inv(l), kind(e), "$x", rcv(l,tg), x b, sendMinimalR{$a:ut2, $tg:ut2}(T; t; l; ds1; ds2; P; Q; d1; d2; f), lnk-inv(l), kind(e), "$x", rcv(l,tg), x  dom(f), IdDeq, @i(x:T), f(x), dom(f), IdDeq, @i(x:T), f(x),  x.A(x), discrete(i;x), vartype(i;x), val(e), (state when e), state@i, x.A(x), discrete(i;x), vartype(i;x), val(e), (state when e), state@i,  T, e T, e  loc e' , Atom$n, sender(e), source(l), P loc e' , Atom$n, sender(e), source(l), P    Q, P Q, P   Q, isrcv(e), A c Q, isrcv(e), A c B, lnk(e), destination(l), lnk_rcv{lnk_rcv_compseq_tag_def:ObjectId}(tg; l), let x,y = A in B(x;y), #$n, (discrete state when e), i B, lnk(e), destination(l), lnk_rcv{lnk_rcv_compseq_tag_def:ObjectId}(tg; l), let x,y = A in B(x;y), #$n, (discrete state when e), i  j < k, case b of inl(x) => s(x) | inr(y) => t(y), (discrete state after e), State(ds), discrete state@i, j < k, case b of inl(x) => s(x) | inr(y) => t(y), (discrete state after e), State(ds), discrete state@i,  , t.1, A , t.1, A  B, s ~ t, loc(e), SQType(T), {T}, {x:A| B(x)} , if b then t else f fi , R-Feasible(R), es realizer ind, False, Normal(ds), B, s ~ t, loc(e), SQType(T), {T}, {x:A| B(x)} , if b then t else f fi , R-Feasible(R), es realizer ind, False, Normal(ds),  x x dom(f). v=f(x) dom(f). v=f(x)   P(x;v), Dec(P), a:A fp P(x;v), Dec(P), a:A fp B(a), EqDecider(T), EOrderAxioms(E; pred?; info), kind(e), type List, Msg(M), val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), e < e', r B(a), EqDecider(T), EOrderAxioms(E; pred?; info), kind(e), type List, Msg(M), val-axiom(E;V;M;info;pred?;init;Trans;Choose;Send;val;time), e < e', r  s, s,  , kindcase(k; a.f(a); l,t.g(l;t) ), , kindcase(k; a.f(a); l,t.g(l;t) ),   x. t(x), x. t(x),   x,y. t(x;y), IdLnk, constant_function(f;A;B), <a, b>, loc(e), x,y. t(x;y), IdLnk, constant_function(f;A;B), <a, b>, loc(e),  A, first(e), suptype(S; T), Type, S A, first(e), suptype(S; T), Type, S  T, Top, T, Top, 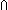 x:A.B(x), Void, Unit, SWellFounded(R(x;y)), pred!(e;e'), x:A.B(x), Void, Unit, SWellFounded(R(x;y)), pred!(e;e'), 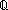 , Id, EState(T), f(a), ES, {i..j , Id, EState(T), f(a), ES, {i..j }, True, a < b, }, True, a < b,  e@i. P(e), e@i. P(e),  e@i.P(e), P e@i.P(e), P  Q, left + right, @i stable state.P(state) , Q, left + right, @i stable state.P(state) ,  b, b,  , @i discrete ds, , @i discrete ds,  , P & Q, x:A , P & Q, x:A  B(x), P B(x), P   Q, valtype(e), s = t, Knd, E, @i state ds, x:A Q, valtype(e), s = t, Knd, E, @i state ds, x:A  B(x), t B(x), t  T, Consistent(R;es), T, Consistent(R;es),  x:A. B(x), f o' g, weak-send-do-apply(es;T;l;tg;a;ds;f), mu'(P), weak-send-do-apply-realizable, es-realizer(p), A x:A. B(x), f o' g, weak-send-do-apply(es;T;l;tg;a;ds;f), mu'(P), weak-send-do-apply-realizable, es-realizer(p), A  B, [car / cdr], [], weakSendDoApplyR{$a:ut2, $tg:ut2}(T; t; l; ds; f), Realizer, discrete-weak-precond-send-p(es;T;A;l;tg;a;ds;P;f), tl(l), l[i], i B, [car / cdr], [], weakSendDoApplyR{$a:ut2, $tg:ut2}(T; t; l; ds; f), Realizer, discrete-weak-precond-send-p(es;T;A;l;tg;a;ds;P;f), tl(l), l[i], i  z j, i <z j, hd(l), e c z j, i <z j, hd(l), e c e' e' |
| Lemmas | send-minimal-lemma, subtype rel self, subtype rel transitivity, select member, weakSendDoApplyR wf, R-sub-Rlist, R-sub-implies, es-real-implies, weak-send-do-apply-realizable, R-consistent wf, unit wf, top wf, first wf, assert wf, not wf, constant function wf, EState wf, kindcase wf, Knd wf, rationals wf, bool wf, qle wf, cless wf, val-axiom wf, nat wf, Msg wf, loc wf, kind wf, IdLnk wf, EOrderAxioms wf, deq wf, Id sq, es-dstate-subtype, es-dstate-after wf, false wf, true wf, es-dstate-when wf, le wf, int seg wf, es-loc wf, existse-at wf, Knd sq, es-kind-rcv, es-isrcv-loc, nat properties, es-sender wf, es-loc-rcv, es-loc-pred, IdLnk sq, es-le-loc, ldst wf, lsrc wf, es-state-subtype2, es-state-when wf, es-val wf, lsrc-inv, ldst-inv, squash wf, alle-at wf, es-vartype wf, es-isconst wf, ifthenelse wf, es-stable wf, fpf-trivial-subtype-top, fpf-ap wf, es-dtype wf, id-deq wf, fpf-dom wf, rcv wf, es-kind wf, lnk-inv wf, es-dstate wf, es-dds wf, es-state-type wf, event system wf, es-valtype wf, subtype rel wf, es-E wf, implies-es-real, sendMinimalR feasible, sendMinimalR wf, Id wf, fpf wf, decl-state wf, bnot wf, decidable wf, normal-ds wf |